Skip to main content

函数渲染器 EquationRenderer

提示

该粒子特效已实现 Playable 接口, 支持按 period/tick 进行播放 可以调用以下三个方法

  • play() 若特效类已经实现 Playable 接口, 则会出现该方法
  • alwaysPlay() 可以使得当前的特效一直进行步进播放, 只不过 ParticleLib 会占用主线程来执行计算
  • alwaysPlayAsync() 跟 alwaysPlay 一样, 只不过 ParticleLib 会使用异步的方式来执行计算并显示特效

函数渲染器即为开发者通过给定一个函数与相关参数, EquationRenderer 则会把函数图像给描绘出来

提示

函数渲染器支持设定的相关参数包括

  • 参数的步进
  • 参数的最大最小值
  • 等

一般函数渲染器和极坐标函数渲染器 都是以 XY 平面作为水平面, 想改的话可以自行更改源码, 参数方程渲染器支持 x y z 三个坐标都给定函数

普通函数渲染器

一般函数渲染器是基于 y = f(x) 的函数进行的渲染

例如简单的 y = x^2 则为抛物线可见如下的实现

GeneralEquationRenderer renderer = new GeneralEquationRenderer(player.getLocation(), x -> {
    return Math.pow(x, 2);
});
renderer.alwaysShowAsync();

实际效果为:

普通方程渲染器5

图中的红点为 player.getLocation 的点, 即原点

由于普通函数渲染器默认参数为

  • minX: -5 表示函数中 x 的最小值
  • maxX: 5 表示函数中 x 的最大值
  • dx: 0.1 表示函数中 x 的改变量, 即每一次显示粒子时的改变量

因此在上图看出来的函数图像比较的高且密集, 因此我们可以修改一下参数可得下面的结果

GeneralEquationRenderer renderer = new GeneralEquationRenderer(player.getLocation(), x -> Math.pow(x, 2));
renderer.setMinX(-3)
        .setMaxX(3)
        .setDx(0.3);
renderer.alwaysShowAsync();

普通方程渲染器3

参数方程渲染器​

参数方程渲染器 支持 x y z 三轴(MC中)都给定方程, 即可以实现

x = f(t)
y = g(t)
z = h(t)

默认 t 的取值范围为 [0, 360] dt 为 1

以下例子都实现于XY平面当中

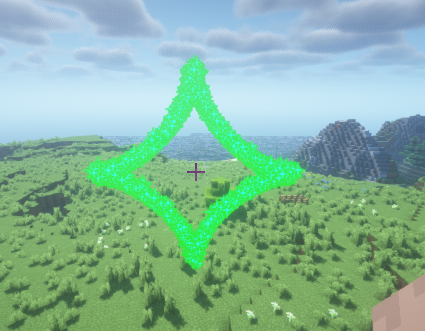
ParametricEquationRenderer renderer = new ParametricEquationRenderer(player.getLocation(), t -> 2 * Math.pow(Math.cos(t), 3), t -> 2 * Math.pow(Math.sin(t), 3));
renderer.alwaysShowAsync();

星形线

ParametricEquationRenderer renderer = new ParametricEquationRenderer(player.getLocation(), Math::cos, Math::sin);
renderer.setDt(30);
renderer.alwaysShowAsync();

圆的参数方程

极坐标方程渲染器​

提示

极坐标支持设定的参数为

  • minTheta θ 的最小值, 默认为 0
  • maxTheta θ 的最大值, 默认为 360
  • dTheta θ 的该变量, 默认为 1

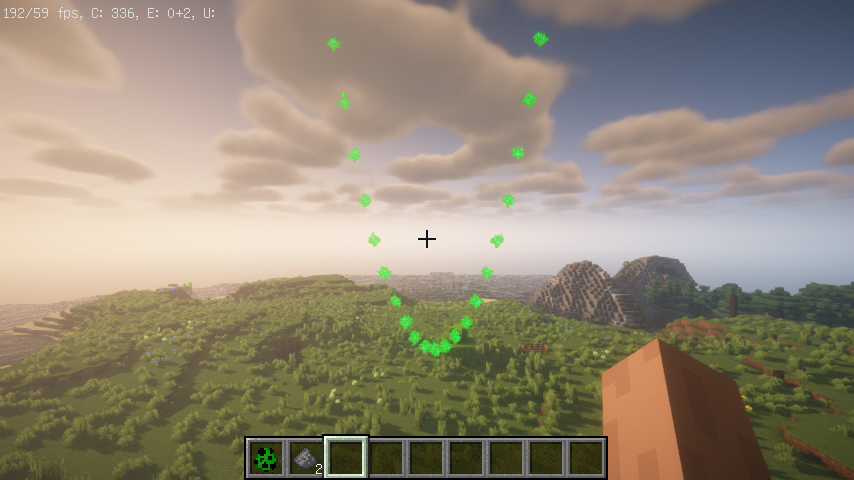
以四叶玫瑰线为例 ρ=a*sin(2θ) 取 a 为 1.5 则有如下图像

PolarEquationRenderer renderer = new PolarEquationRenderer(player.getLocation(), theta -> {
    return 1.5 * Math.sin(2 * theta);
});
renderer.alwaysShowAsync();

四叶玫瑰线